Táčky u geometrie
Výsledky
Úkoly:
-
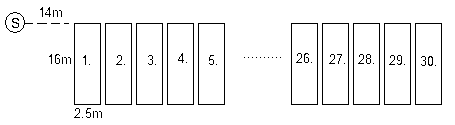
V zahradě je 30 záhonů. Každý má délku 16 m a šířku 2,5 m. K zalévání nosí zahradník vodu ve vědrech ze studny vzdálené 14 m od zahrady, při čemž obchází záhony o mezích. Najednou přinese vodu na jeden záhon.
Kolik metrů ujde, než zaleje všechny záhony? Cesta začíná a končí u studně
-
Jakou silou působí na povrch Země vzduch, který ji obklopuje? Pokuste se to odhadnout přibližně. Stačí znát zemský poloměr a vědět, že za normální tlak vzduchu při Zemi je zhruba 1 atmosféra.
-
Umíte sestrojit trojúhelník, jsou-li dány jeho tři výšky?
-
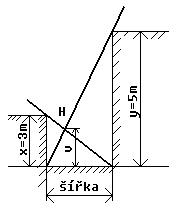
V příkopu podle obrázku, na jehož šířce nezáleží, stojí dva žebříky, které se opírají v rozích a na okrajích.
Jak vysoko je průsečík H obou žebříků?
-
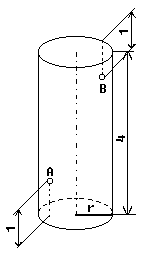
Na válcové nádrži, která má obvod 6 m a výšku 4m, máme spojit drátem kontakt A (na vnějším povrchu) s ukazatelem výšky hladiny B (na vnitřním povrchu), kde body A a B leží v rovině obsahující osu válce. Jaká je nejkratší možná délka spojovacího drátu, který se vine po stěně nádrže?
-
Podle Eulerovy věty postačující podmínko k tomu, aby se daný souvislý obrázek dal nakreslit jedním tahem, je, aby tento obrázek obsahoval právě dva vrcholy libovolného stupně nebo aby neobsahoval ani jeden takový vrchol. (Vrcholy budeme v tomto případě nazývat všechny průsečíky stran, úhlopříček, jakož i body, z nichž vychází právě jedna čára. Počet čar, jež vycházejí z nějakého vrcholu, nazýváme stupněm tohoto vrcholu.)
Na základě uvedeného zjistěte, zda je možno narýsovat:
a) obdélník ABCD a v něm úhlopříčku AC jedním tahem;
b) pravidelný šestiúhelník se všemi jeho úhlopříčkami.
-
Máme vést přímku danými body. Je to jistě nejjednodušší konstrukční úloha - za normálních okolností. Ale my máme k dispozici jen kružítko a pravítko, které je kratší než vzdálenost bodů.
Jak vyřešíme tuto úlohu pomocí pravítka (s měřítkem) a kružítka?
-
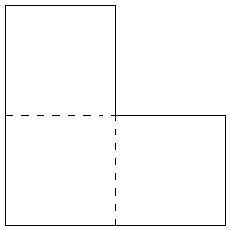
Pozemek na obrázku je třeba rozdělit na 8 stavebních parcel tak, aby měly týž tvar i velikost a součastně aby se na každé dal postavit dům.
-
Čtverec lehce rozdělíme na 4 shodné čtverce, na 4 shodné pravoúhlé trojúhelníky i na 8 shodných trojúhelníků.
Dokážete ho však rozdělit na 6 obsahem i tvarem shodných částí? Jaký budou mít tvar?
Výsledky



