Jaký čas by byl k tomu zapotřebí?
(Objem Slunce je 1027 m3 a čtyřicáté pokolení nálevníků, které nezahyne má objem 1 m3 )
Kolik vody (tekutiny) asi vypije člověk za celý život? (Předpokládáme, že žije průměrně 60 let a denně vypije asi 1,5 litru různých tekutin.)
x + y = 2
xy - z2 = 1.
Podle toho je možné vypočítat, kolik zlata a kolik stříbra obsahovala koruna. Připomínáme, že měrná hmotnost čistého zlata je 19,64 a stříbra 10,5.
Nechť a a b jsou dvě stejná čísla, tj. a = b. Vynásobme obě strany rovnice číslem a, dosateme a2 = ab. Odečteme od levé i pravé strany rovnosti číslo b2 . Dostaneme a2 - b = ab - b2 . Jestliže obě strany rovnosti rozložíme na součiny (a + b)(a - b) = b(a - b) a obě strany dělíme výrazem a - b, dosatneme a + b = b. Jestliže b = a, můžeme v poslední rovnosti nahradit číslo b číslem a a dostaneme a + a = a čili 2a = a. Jestliže tuto rovnost dělíme dvěma, dostaneme a = a/2, což znamená, že celek se rovná své polovině.
Vysvětlete chybu v úvaze.
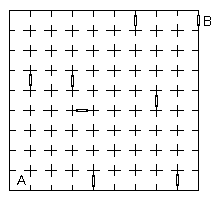
Abychom se dostali ven, je nutné nejdříve přemýšlet a připravit plán postupu. Najděte ho. Začínáme v A a vycházíme v B.
95 % dní bylo chladno,
85 % dní pršelo,
75 % dní bylo zamračeno,
65 % dní bylo bezvětří.
Z uvedených údajů máte vypočítat, kolik procent bylo takových dní, kdy bylo současně chladno, oblačno, bezvětří a pršelo.